Golden Ratio
What makes a single number so interesting that nearly everyone from scientist to the artist would write about it? What is so special about the golden ratio? This golden number, 1.61803399, represented by the Greek letter Phi, is known as the Golden Ratio.
It goes by many names, golden mean, divine proportions, golden section, etc. which implies that it has been discovered and rediscovered many times throughout history. Egyptians used both pi and phi in the design of the Great Pyramids. Da Vinci’s The Last Supper was based on the Golden Ratio. Not only Da Vinci but Michelangelo, Raphael, Botticelli, Burne Jones and many more have used the golden ratio to bring harmony and balance in art and design.

Square

5:4

4:3

Silver Ratio

Golden Ratio

Platinum Ratio

16:9

Bronze Ratio
This Golden Ratio truly is unique in its mathematical properties and pervasive in its appearance throughout nature. Where Pi (3.14) is the ratio of the circumference of a circle to its diameter, Phi or Φ (1.618) is the Golden Ratio that results when a line is divided in one very special and unique way.
Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The irrational number (1 + √5)/2, often denoted by the Greek letter ϕ or τ, which is approximately equal to 1.618 is golden ratio.

0
nth Term
0
n-1 th Term
0
n
0
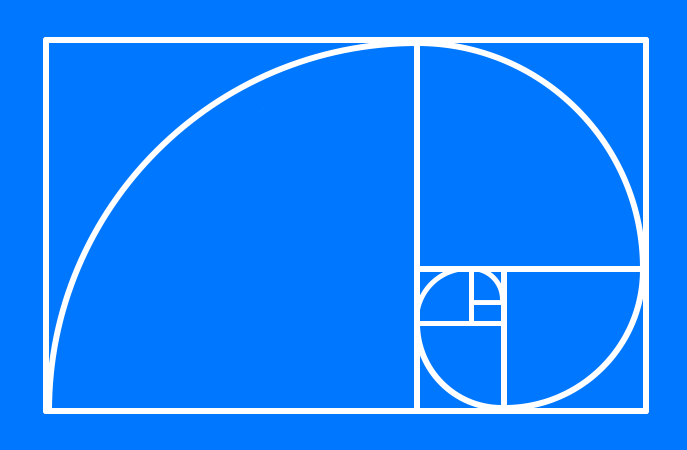
From the experiment above we come to know that dividing subsequent terms of Fibonacci sequence results in the golden ratio. The further you go in the series, the closer the result gets to Phi. If you go further into the series and you’ll find that 233/144 = 1.61805, a very close approximation of Phi, which to ten decimal places is 1.6180339887.
Golden Ratio can be written in many forms. Here are few of them
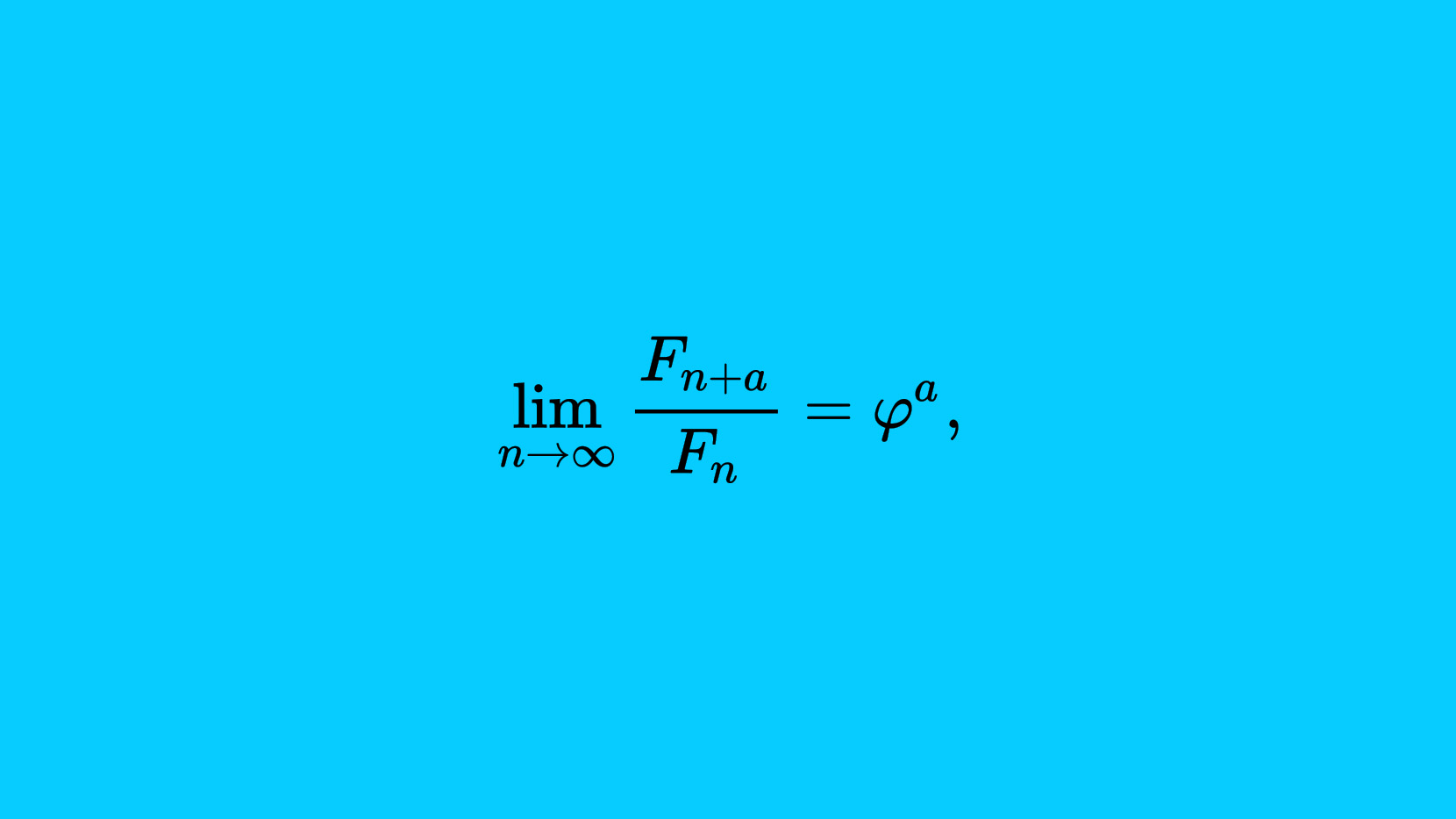
Phi is the only number whose square is greater than itself by one, expressed mathematically as Φ² = Φ + 1 = 2.618.
Phi is also the only number whose reciprocal is less than itself by one, expressed as 1/Φ = Φ – 1 = 0.618.
The Golden Ratio is also equal to 2 × sin(54°), interesting isn't it?
There are many other fascinating mathematical relationships and oddities in both Phi and the Fibonacci series that can be explored in more depth, but for now let’s now take a step away from the purely mathematical and venture into nature, where Phi and the Fibonacci series manifest themselves pervasively, but not universally. Fibonacci numbers frequently appear in the numbers of petals in a flower and in the spirals of plants. The positions and proportions of the key dimensions of many animals are based on Phi. Examples include the body sections of ants and other insects, the wing dimensions and location of eye-like spots on moths, the spirals of sea shells and the position of the dorsal fins on porpoises. Even the spirals of human DNA embody phi proportions.

Angle
1
Pattern Color
Background Color
* Try Changing the value to golden ratio i.e. 1.618 and see if it forms Sunflower like pattern.
* You can also drag the pattern.
* You can also save the image by right clicking on it.
Slider
0
Fill Color
Stroke Color